There is a standard disclaimer in financial journalism and marketing: Past performance does not indicate / guarantee / predict future results. Just because a particular company / investment trust / mutual fund has performed well in past years, it need not follow that it will do so in the future. So as someone writes about that past performance they are obliged to remind you not to assume next year will necessarily be the same.
A few days ago, I published a post looking at what happens next after the S&P 500 index has a negative year.
It was prompted by a Bloomberg article entitled S&P 500 Facing a Historical Warning Sign After This Year's Slump, which was referenced in a tweet. This prompted me to do a little fact checking, seeing whether the figures and statistics from past years back up the claims they made. By way of reminder, there were essentially 3 claims being made
- Claim 1: The tweet and the article both said that a year in which the S&P 500 declines is only rarely followed by another year in the red. In other words, knowing that Year 1 has seen the index drop, year 2 is less likely to drop than would have been the case otherwise.
- Claim 2: The tweet said that if the S&P 500 does have two consecutive years in the red, people should then brace themselves for another difficult 12 months. Given you can only brace yourself in this way once you know the second 12 months have also seen decline, this suggests that the third twelve months will also be red once you know the first and second years were.
- Claim 3: The article said that when there are two down-years in a row, the second of those two years is typically down by more than the first of them.
It may be that claims 2 and 3 are really the same, with the tweet being poorly worded. As I say, you can't brace for another difficult 12 months until you know you're in the scenario when you have two red years in a row. But it may be that the tweet only meant to say the same as claim 3 — by the end of the second red year, you'll probably have had a worse time in the last 12 months than in the first.
In my previous post, I only looked at the black and white, on or off, boolean, indicators. This was the way their headline claims were worded: "the chance of a second year in the red after a first year in the red". So I just looked at the probabilities that a year was red or green, up or down. And, for claim 3, I just looked at the probability that year 2 was down by more than year 1. I did not look at how much any given year was up or down. I also did not look more widely at whether there was any correlation between one year and the next.
So, in this follow-up post, I want to look at the numbers. This is important. Claim 3 says that when you do get two down years in a row, it is likely that the second will be worse than the first. My previous post established that there is statistically significant evidence to back this up, but the evidence for claim 1 was not statistically signifiant. However, claim 3 means that when the second year is down it is badly down. So we are not looking at a scenario where the second year is up or down by about the same amount; we are now possibly comparing a large loss with a small gain, and this may make for a loss on average.
So let's look at the numbers by drawing some charts that compare one year to the next. This will illustrate, graphically, those 3 claims above. And let's look at the statistics of the actual returns, not just whether it's above or below the zero line. And let's see what we see.
Disclaimer: The scatter diagrams below were drawn using the data available when I prepared the first article. At that point, it looked like 2022 would be down by 18%. In the end, it closed down 19.4%, so the 2021/2022 marker is not quite in the right place. The small adjustment would not affect any of the statistical calculations that follow.
A diagram of the data
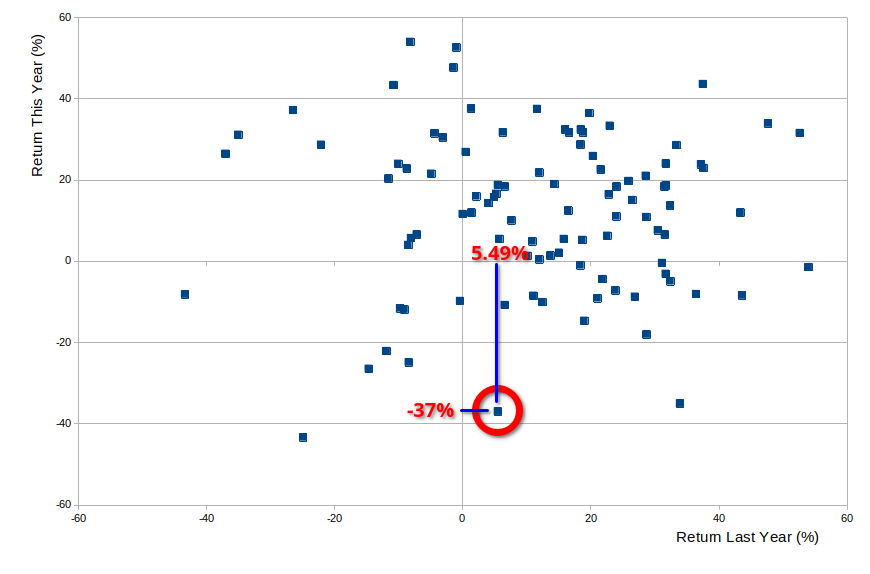
Here is a scatter diagram. Each point represents a pair of consecutive years. The X-axis (horizontal) shows the return of the S&P 500 in one year; the Y-axis (vertical) shows the return the following year. The units are percentage points.
So, for example, in 2007, the S&P 500 was up by 5.49%. In 2008, the year after, it was down (a staggering) 37%. We can see this point on the chart as indicated below. The point is at 5.49% on the X axis (one year's return), and at -37% on the Y axis (the following year's return):
Claim 1: Down years less likely to be followed by a second one
In terms of our diagram, the claim is that when one year is down (when we're on the left hand half of the chart). we are relatively unlikely to be down the following year (that is, to be on the bottom half of the chart).
That's to say: Look at the proportion of the points that are in the bottom half of the chart, compared to the top half. Now just look at the left hand half of the chart: the proportion of points in the bottom left, compared to the top left, is smaller.
We can draw this as follows:
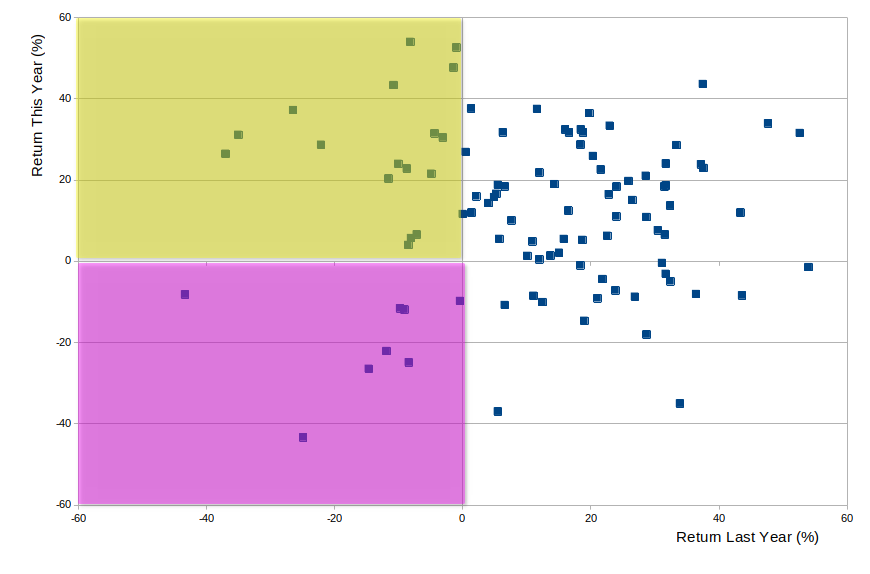
The purple area is sparse compared to the yellow (and is more so than the bottom half as a whole is compared to the top half as a whole).
We found in the previous post that this is not the case. Or, more precisely, any difference is not statistically significant.
But what if we don't just look at how many points are in each box (are we "up" or "down") but where the points lie (how much we are up or down)? If we know we are in the left hand half of the diagram, will we (on average) see a higher return next year because of this?
The average (mean) return from 1927 to 2022 is 12.02%. The standard deviation of these returns is 19.88%.
We noted last time, there are 25 data points on the left hand half of the diagram (where the year before saw a loss). So we need to look at the average return of those 25 data points and see if it is higher than 12.02% by an amount that is statistically significant.
The average of those 25 data points is 13.19%. That is higher than 12.02%, but is the increase statistically significant?
We're now looking at the average of a sample of 25 data points. Such an average will have a standard deviation that is smaller than that of the whole set by the square root of 25, so we need to divide our overall standard deviation by 5. This gives us a standard deviation of 3.975% (19.88% ÷ 5).
13.19% is 1.17% lower than 12.02% (13.19% - 12.02% = 1.17%). One standard deviation was 3.975%. 1.17 ÷ 3.975 = 0.295. So 1.17% is 0.295 standard deviations. So we are higher than 12.02% by 0.295 standard deviations.
We talked last time about confidence intervals. We said that statisticians normally (sic.) look for a minimum of 95% confidence. To be an outlier, the data before us has to only occur 5% of the time when nothing different is going on. This needs the sample to be at least 1.96 standard deviations away. We also said last time that for 90% confidence (generally too low to really count as statistically significant) your sample needs to be at least 1.64 standard deviations away.
But here we are only 0.295 standard deviations away. This is very far from being statistically significant. If the left hand half of the chart (years following a down-year) followed the same distribution of the chart as a whole, you'd get the kind of returns we are seeing really often.
How often? If 1.96 standard deviations means you're seeing an event that would only occur 5% of the time, 0.295 standard deviations means you're seeing an event that would occur 76.8% of the time. If you ran the S&P 500, for 95 years 4 times in a row, following a pattern where being down one year made you neither more nor less likely to be down the year after, you'd expect to see the this kind of data 3 out of 4 times. There's nothing to see here.
Conclusion: Even looking at how much we gain or lose, there is no evidence to support claim 1.
Excursus: Correlation
Let's return to something I specifically said I hadn't covered in the earlier post. There, I just looked at whether being red or green one year had any bearing on whether you would be red or green the following year. In this post, I'm looking at the actual return figures, so this is a good point to look at the subject of correlation.
Is there any evidence that there is a correlation between the S&P500 returns one year and the returns the following year?
To answer this, we need to look at something called the "correlation coefficient". The idea here is that you fit the best straight line you can to the chart above. You then look at how closely the points follow that line. You end up with a score. A score of 1 would indicate that the points are a perfect fit, each one exactly on the trend-line, and the trend-line slopes upwards. A score of -1 would also indicate a perfect fit, sloping downwards. A score of 0 would indicate that there is no trend-line at all; the points fit totally evenly around any line you try to draw. Any real-world data will not have a correlation coefficient of exactly 1, -1 or 0. Instead, you may get a figure like 0.8, indicating a pretty good (but not perfect) fit to an upward sloping line.
You may have guessed that we can then look at statistical significance: How far away from 0 does the correlation coefficient need to be before there is evidence that the data is following a trend? We'll get to this part once we've looked at the correlation coefficient itself.
The correlation coefficient for this set of data is -0.004. That's minus 1/250. You'll notice that is very close to zero, so the data is almost perfectly scattered.
Is this statistically significant? You'd guess not, and you'd be right. To work out whether apparent correlation is statistically significant you perform a test called a "T Test". This turns that correlation coefficient into a probability. If you were dealing with a randomly scattered universe of data, how unlikely would the data you have observed be? In our case, the probability comes out at 91.4%. That's to say, 91.4% of the time you'd see something rather like this. For there to be statistically significant evidence that the data correlates along a straight line, you'd want 5% or less — that's to say, random data would only come out along this kind of straight line 5% of the time. We are almost as far from that as it's possible to be.
Conclusion: There is no statistical evidence of any correlation between one year's S&P 500 return and the return the following year.
Comparison: Dow Jones versus S&P 500
Before we leave correlation, let's look at a different set of data: The performance of the Dow Jones Industrial Average (a share-price weighted index of 30 stocks) with the S&P 500 in the same year. You'd instinctively expect that the S&P 500 has a good year when global stocks in general did well, and in particular when US stocks did well, and so you'd expect those to be the years when the DJIA did well. In short, you'd expect the returns for those two indices to be broadly correlated.
Here's the same type of scatter diagram comparing the year-on-year returns of those two indices:
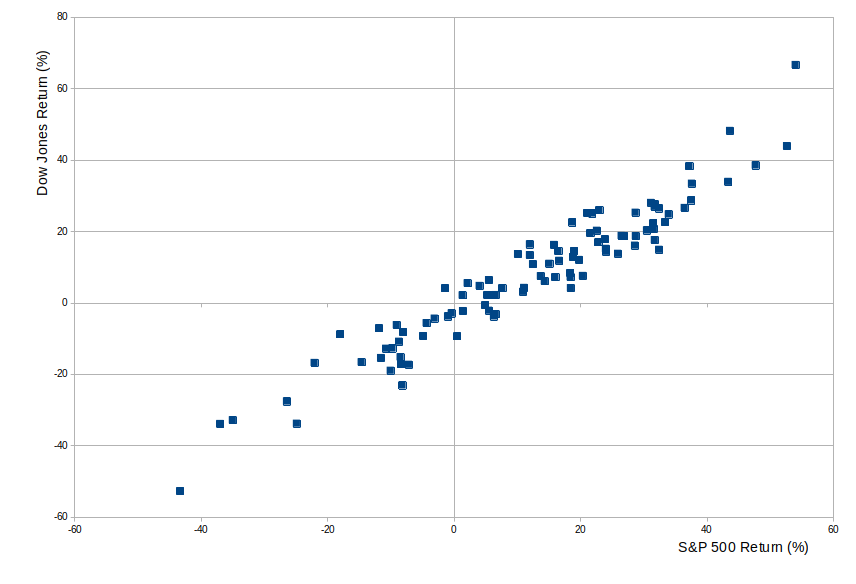The human eye can see there's a strong correlation here, which is what we expected.
So, to give you something to compare the figures above, when we were looking at the returns on the S&P 500 in two adjacent years:
The correlation coefficient here is 0.957, comfortably close to 1, and very different from the 0.004 we had before!
The T-Test, done with the assumption we were expecting and testing for a positive correlation here, shows 5.93%. That's to say, if the SPX and DJIA were totally uncorrelated, the probability of getting a scatter diagram with this much correlation is 5.93%. Interestingly, a rigorous statistician insisting on 5% or 2.5% probability would still rule that this is not sufficiently correlated to conclude there is a pattern. But the contrast with the S&P 500 in successive years is clear to see.
While we have this data here, in case anyone is interested, the slope or gradient of the trendline here is 0.93. That's interesting. It is less than 1. That means that as the S&P performance grows stronger, the Dow does not grow quite as much. Conversely, in the down years, the Dow doesn't accelerate its losses quite as fast as the S&P 500. More calculations would be needed before anyone should choose their ETFs off the back of this, but it suggests the S&P is a higher risk, higher return index, the Dow ever so slightly safer and therefore ever so slightly less outperforming in the good years.
The intercept of the trendline is at -3.5%. That's to say, typically, if the S&P ends the year flat, the Dow would decline by 3.5%. If the Dow is flat, the S&P on average would gain 3.3% (because the gradient isn't 1).
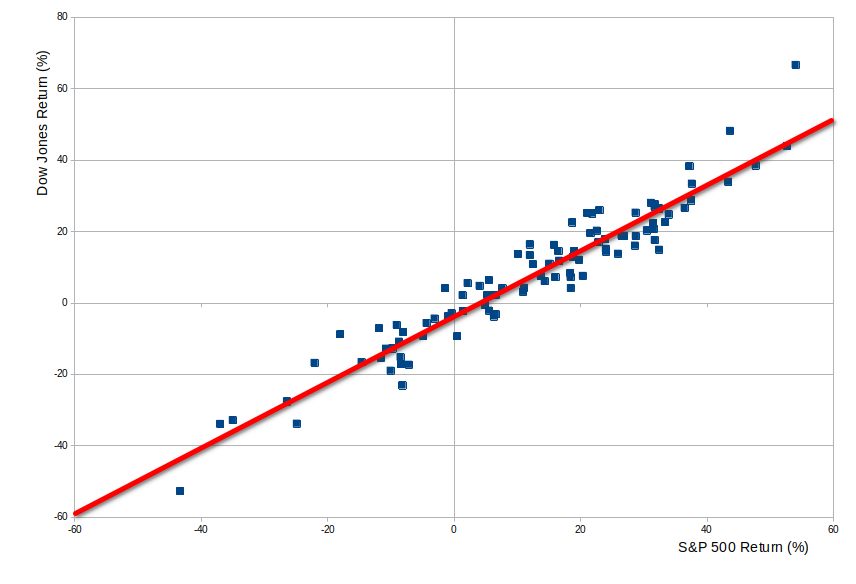
Anyway, back to the S&P 500, and its performance in successive years.
Claim 2: Two bad years are likely to be followed by a third
We saw there is no evidence for this, but we can now draw a diagram of what is claimed.
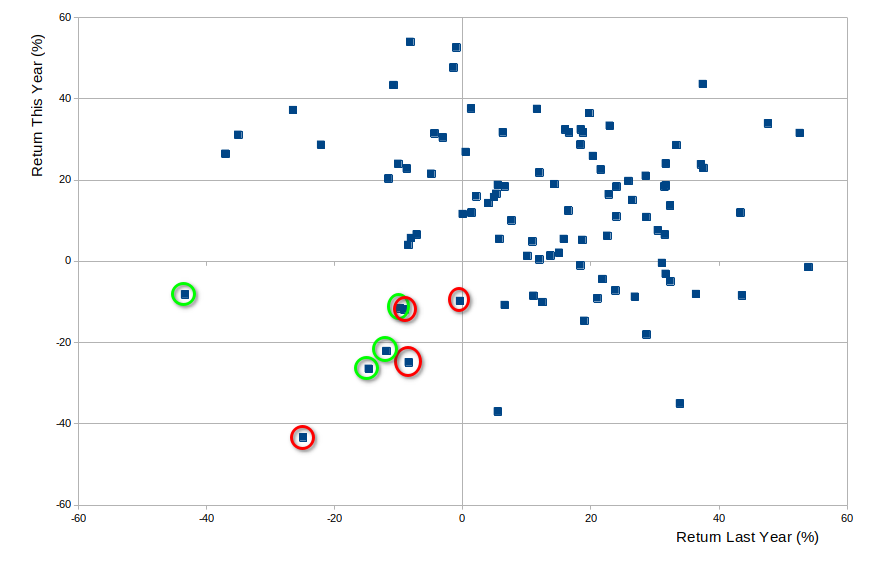Recall from the previous post: there were 8 occasions when the S&P 500 fell two years in a row.
The chart above shows us this: There are 8 data points in the bottom left quarter of the diagram (when both "last year" and "this year" showed a return below zero).
We can then look at what happened in the third year, the year following the double-drop. If the third year was also a decline, we draw a red circle around the data point. If the third year saw the S&P 500 rise, we draw a green circle.
You can now see in the diagram what we reported last time: The third year was up 4 times, and down 4 times. The statistical calculations were in the previous post, but the conclusion:
Conclusion: 4 out of 8 is not statistically significant evidence that two negative years are more likely to be followed by a third.
Claim 3: When there are two down years in a row, the second can be expected to be down by more than the first
Again, we can now see this in the diagram. Recall: There were 8 occasions when the S&P 500 fell two years in a row.
We can draw a diagonal line from the origin of the diagram, heading exactly south-west, down and left at exactly 45 degrees. If the point is below this line, then the second year saw a sharper decline than the first year. If the point is above this line, then the first year saw a sharper decline than the second year.
Here is that diagram:
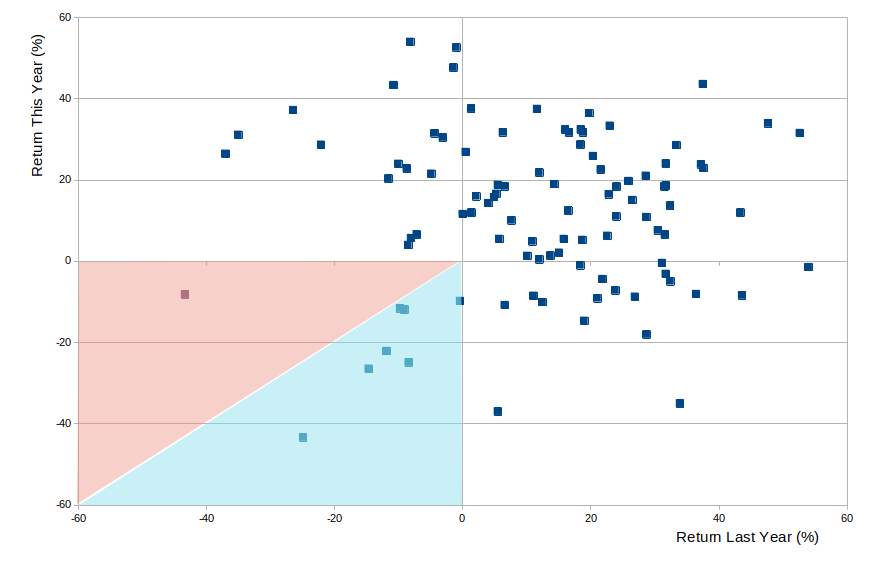
You can see that in 7 of the 8 years, we are in the blue zone, where the second year saw the larger decline. In just 1 of the 8 years are we in the red zone, where the first year saw the larger decline. We noted that 7 out of 8 is statistically significant.
Drawing a diagram allows us to see that some of those blue points are fairly close to the diagonal line. Once again, let's go beyond just looking a how many points were blue rather than red; let's look at by how much the second year was worse (or better) than the first.
This changes things. On average, the percentage drop in the second year exceeded the percentage drop in the first year by 4.47%. The standard deviation of that excess drop, adjusted for the small sample size we have, is 17.03%. So the second year is down more than the first by 0.26 standard deviations.
(Even if we treat the one point in the red zone as an outlier, the standard deviation of the remaining 7 points is 6.27%. So 4.47% is still only 0.71 standard deviations.)
We've been here enough times before that you don't need me to tell you: we need a difference more like 1.96 standard deviations before this is statistically significant.
Conclusion: When we look at how much the second of two decline years is worse than the first, we see that there is no statistical evidence to say that the second year will be worse than the first.
Overall Conclusion
The Bloomberg headlines grabbed attention. They tap into what people wish to be true. After a bad year for the markets in 2022, people enter 2023 wanting someone to tell them there is evidence 2023 will be better. Sadly, one year's performance is almost perfectly uncorrelated to the next. There is no evidence to back this up.
People are also captivated by sensational facts. The idea that when things are worse they're getting successively worse is not welcome good news, but it makes for a little excitement. Happily, there is also no evidence to back this up.
2023 will do what 2023 will do. Illness, war, raw material shortages, political unrest around the world, productive economies, rising employment, demand for housing, capacity for disposable income: all these things will shape the global economy. Stock markets try to price in known future factors too, so no human can reliably predict whether markets will rise or fall. Ultimately, God is in charge of everything, even the decisions freely taken by several billion human beings, and not a hair falls to the ground apart from his good purposes.
Past performance does not indicate / guarantee / predict future results. Even for the S&P 500. Whatever Bloomberg's editors may write. Plan your decisions according to principles of good stewardship, manage risks responsibly, set your priorities in the light of eternity, then trust God to take care of his children.
Add new comment